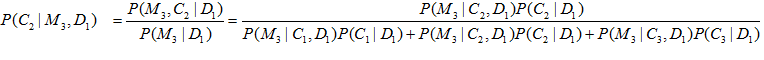The Collapsed Wavefunction: Your intuition is WRONG

Showing posts with label Your intuition is WRONG. Show all posts

Wednesday, January 16, 2013

The Monty Hall Problem and a lesson in statistics

This semester I am the teaching assistant for a graduate level course on Statistical Mechanics. To me this represents a milestone. Just a little over two years ago I was in the department's office nearly in tears (okay, actually in tears). I was prepared to quit the program - I was just too stupid for graduate school (I'm still not sure I am smart enough, but that's the subject for another blog). It was only my second week in grad school and already I was convinced that I would never pass Statistical Mechanics.

I don't shed tears over Stat Mech anymore, in fact it's probably one of my favorite classes. Statistical Mechanics is the branch of chemistry (or physics, depending on who you ask) that applies large number statistics to molecules. Since molecules are small and there are so many of them the statistics work out nicely and we can accurately predict thermodynamic quantities (like pressure, energy, entropy, etc).

While brushing up on the subject I was reminded of an interesting statistical problem that I thought I'd share. It's called The Monty Hall Problem, and it's based on the game show "Let's Make a Deal!"

Monty Hall was the original host of "Let's Make a Deal!". Most of the game show worked by giving someone in the audience a small prize and then offering them a deal. "Keep the small prize or trade it for whatever is behind door # 1!". Sometimes door #1 got you a new car other times it was something completely useless. So here's the Monty Hall problem:

Suppose Monty shows you three doors. You know that behind one of the doors is a new car. Behind each of the other doors is a goat. You choose a door at random (we'll say door #1). Then, Monty opens door #3 and reveals a goat. Monty then makes you an offer - You can switch and take what's behind door #2 instead of door #1. Should you switch or stick with your initial choice?

At first it may seem like switching will make no difference. When the game began your odds of winning a car were 1/3. Monty opens a door and reveals a goat, but that still leaves one goat and one car. The odds must be 50/50, right? The car must be equally likely to be behind either one of the doors. It's often the case, though, that your intuition will deceive you. Already this semester I have warned several students that they were trusting their own intuition a little too much.

The real answer to the Monty Hall problem is that by switching your choice you move from a 1/3 chance of winning a car to a 2/3 chance. It's important to note that Monty knows where the car is and will never open a door to reveal it (that would ruin the game). Below I outline three ways of convincing yourself that this is the answer. Choose your favorite.

Thinking it through: Making a table
In the beginning of any statistics class you'll get some very easy problems. For example:

"If I roll a 6-sided die¹ what are the chances that I roll a 6?"

These problems are usually pretty easy to answer by just thinking about it or in some cases writing down all the possible outcomes and counting them. Let's write out all the possible outcomes for the Monty Hall problem. This table assumes your choice was door #1 and that Monty will eliminate one of the other doors that has a goat.

Behind Door #1	Behind Door #2	Behind Door #3	Your prize (No switching)	Your prize (Switching)
Car	Goat	Goat	Car	Goat
Goat	Car	Goat	Goat	Car
Goat	Goat	Car	Goat	Car

Just by writing out all the possible outcomes you can see that switching gives you a 2/3 chance of winning a car while not switching leaves you with a 1/3 chance. It can be tedious to write out all the possible outcomes to a problem, especially when you have a large number of events. But that's why we have math.

Mathematically: Bayes' Theorem
Bayes' Theorem is a statistical tool that lets us analyze the probability of one event happening given that another event has already occurred. In this case, what is the probability that the car is behind door #1, given that Monty reveals a goat behind door #3. The math behind Bayes' theorem is written as:

$P(A|B) = \frac{{P(B|A)P(A)}}{{P(B)}}$

Which is read "The probability that event A will happen given that B is true is equal to the probability that B will happen given that event A has happened multiplied by the probability of A divided by the probability of B."

For the Monty Hall problem we have three important variables. The door you choose (D_n), the door Monty opens (M_n) and the door that actually has a car (C_n). So the probability that the car is behind door #2 (C₂), given that you chose door #1 (D₁) and Monty opened door #3 (M₃) is:

Which works out to be:

So, if you choose door #1 and Monty reveals door #3 there is a 66.6% chance that the car is behind door #2 and only a 33.3% chance that it is behind door #1.

Mathematically: Renormalization

This is my personal explanation of the math. As such it is not strictly correct (a mathematician would likely have my head), but the math works out and it is applicable to many other problems. For this reason I've chosen to include it.

When we first started out door #1, door #2, and door #3 all had equal probability of containing the car (1/3). Then Monty opens up door #3 and reveals a goat. You haven't changed anything, so your probability is unchanged. You still have that 1/3 chance of getting a car if you stick with door #1. However, you do have a choice. You can switch to door #2. If you choose to switch, we have to renormalize the problem. Normalization basically just means that the total probability must be equal to 1. There are a few ways we can normalize.

1. Realize that the remaining probability is equal to the total probability minus the original probability. In this case that means 1-1/3 = 2/3.

2. Divide by the "new probability". In other words our initial probability was 1/3. Now there are only 2 possibilities. We have to renormalize to reflect that change. The probability that the car is in a door other than door #1 is (1/3)/(1/2) = 2/3.

This solution is sure to get me in trouble with mathematicians (they don't like it when you place loose with their maths), but it does work. To convince you that it's not just true for this specific case let's imagine there are N doors. The probability of choosing correctly is 1/N. Monty opens one door and allows us to switch. What is the probability that the car is in one of the other available doors (instead of door #1)? Solving it both ways from above:

1. The total must be one, and I know my original probability is 1/N. The remaining probability is 1-1/N = (N-1)/N.

2. Renormalize. (1/N)/(1/N-1) = (N-1)/N

Renormalization is a handy tool, but you have to be careful. Running about dividing probabilities willy-nilly is sure to get you a bunch of wrong answers. It's important that you know the physical meaning behind the division that you're doing.

Notes

[1] Nerds are very easy to spot. They're the ones that ask "How many sides?" when you talk about dice. Everyone else assumes you're talking about 6-sided dice. After all, isn't that the only kind?

Thursday, December 13, 2012

But I saw it with my own eyes!!

Last week the Oregon supreme court ruled unanimously to change the legal policy on eyewitness identification. The new ruling places the burden of proof that an eyewitness statement should be admitted to court proceedings on the prosecutors instead of the defendants. What does this have to do with science? I'm glad you asked.

Eyewitness testimony is often very wrong - even missing important details. Take for example this video. Can you correctly count the number of times that this basketball is passed between the players wearing white shirts?

How about in this version?

We tend to give more merit to our own memories than we should. We trust ourselves and say things like "I know what I saw". However, even seeing something with your own eyes does not mean that it happened as you remember. Not only do we miss details, but our memories are very malleable - they are easily influenced by time, what other people say, or even what we wish the memory to be. Not only do we trust our own eyes more than we should, but we trust everyone else's eyes more than we should too. The supreme court has even said that:

Despite its inherent unreliability, much eyewitness identification evidence has a powerful impact on juries. Juries seem most receptive to, and not inclined to discredit, testimony of a witness who states that he saw the defendant commit the crime.

Eyewitness testimony is likely to be believed by jurors, especially when it is offered with a high level of confidence, even though the accuracy of an eyewitness and the confidence of that witness may not be related to one another at all. All the evidence points rather strikingly to the conclusion that there is almost nothing more convincing than a live human being who takes the stand, points a finger at the defendant, and says 'That's the one!'

In other words, juries are highly influenced by a confident eyewitness testimony - even though how confident you has nothing to do with how right you are.

One tragic story of eyewitness misidentification is that of Ronald Cotton. In 1984, Jennifer Thompson awoke to a man standing over her bed. A knife was held to her neck and she was raped. During the attack she made a conscious effort to memorize important details of her attacker. Later that day at the police station Thompson was shown six photos. After examining them for several minutes she chose the Ronald Cotton from the photo line-up. "Did I do OK?", she asked the detectives. "You did great" was the response. This positive feedback solidified her confidence that Ronald Cotton had raped her.

Later she was asked to identify Ronald Cotton from a physical line-up. Once again she chose Ronald Cotton (who was the only person in both the photo and physical line-up) and once again her confidence in the identification increased when she was told she picked the "right guy". However, DNA evidence has since cleared Ronald Cotton. Thompson and Cotton have since written a book on their story - Picking Cotton: Our Memoir of Injustice and Redemption.

Cotton's story can help us see how our eyes can easily deceive us. Our own personal memories - no matter how vivid - are not by themselves convincing evidence of anything. That's one reason why scientists use so many measurement techniques. The ones and zeros that the instrument in my lab outputs may seem impersonal, but they don't change over time. I can always go back and reanalyze the data to be sure of what really happened.

If you need more science check out our , follow us on , or check out our .

Sunday, September 30, 2012

30 Second Science: Pareidolia

Pareidolia (Pair-eye-dough-lee-ya) is the phenomenon that causes the human brain to perceive random stimulation as significant. It's the reason why this house looks like it's screaming at you.

and the reason behind seeing this face on the surface of Mars.¹

and the reason why just about any circle with "eyes" and a "mouth" will look like a face, even if it is completely lacking in any real human features.

In fact, let's see how distorted that face can get before you no longer see it as a face.

still a face?

Maybe it looks a little alien, but still a face to me.

Even when I separated the eyes between the mouth it still looks like a face. I see it as two eyes and a long nose if I tilt my head to the right.²

Pareidolia is also what causes something random, like ink in the Rorschach tests, to look like something else.

Oh, sorry. Wrong Rorschach.

Your brain will attempt to interpret the random ink blots in the image above. Supposedly how you interpret the image gives insight into your psychological state, though there are good reasons not to believe that is the case.

The reason you see a face so easily in all of these examples is that you're brain has evolved (there's that pesky "E" word I keep bringing up) to quickly recognize faces. Carl Sagan hypothesized that the ability to recognize faces would be an important survival advantage for early humans. Being able to quickly identify a friend or foe could be the difference between life and death. This idea is related to the idea of a pattern-seeking mind that I have already talked about. The human brain is great at picking out patterns in random noise. Sometimes too good at it.

Related to pareidolia is the phenomenon known as sine wave speech. Matt Davis is a researcher at the MRC Cognition and Brain Sciences Unit. The following clips are from his website. Listen to this audio a few times. It should sound like (to quote my five year old) "a bunch of silly whistles". It may slightly resemble speech, and you may make out a few words, but for the most part it's nonsense (my five year old says he heard it say "I love you"). Now listen to this audio clip, and the original audio clip once more. Suddenly, with this new context, the first audio doesn't just sound like whistles and noise. Instead you can hear, almost clearly, a voice in the whistles. My five year old was able to quickly tell me what the voice was saying when he heard the whistles again. The shocked look on his face was priceless. He knew that his brain had just played a trick on him. I doubt you will hear it as only whistles ever again. Of course, this isn't quite the same as pareidolia. You don't need any perceptual insight to see a face on Mars or in a house. You just need millions of years of evolution to force your brain to see it that way.

Notes

[1] Just to be clear, that is not a sculpture from an ancient human-like civilization on Mars. It is a hill with rocks randomly strewn across it. Your brain interprets this randomness as a face. Higher resolution images have put this controversy to bed long ago - unless you're a conspiracy theorists, then it was all a big government cover up. Also, look behind you. They're watching you.

[2] After I had made this image, the first thing I did was tilt my head to the right. When I showed this to my brother he immediately tilted his head to the right. I wonder how many of you did the same thing. Your brain knew just where the face was, didn't it?

If you liked this article, head over and "like" our .

Monday, February 27, 2012

A Pattern-seeking Mind

Have you heard about the odd similarities between John F. Kennedy and Abraham Lincoln? To name a few:

Both were elected to the House of Representatives in '46
Both were runners-up for their party's nomination in '56
Both were elected to the presidency in '60
Both were succeeded by Southern Democrats named Johnson (who were both born in '08)
Lincoln had a secretary named Kennedy. Kennedy had a secretary named Evelyn Lincoln
Lincoln was warned by his secretary to not go to the theatre. Kennedy was warned by his secretary not to go to Dallas
Both were shot in the head, from behind, on a Friday, and in the presence of their wives
Lincoln was shot in Ford's Theatre, Kennedy was shot in a Lincoln made by Ford
Both John Wilkes Booth and Lee Harvey Oswald were born in '38
Booth ran from a theatre to a warehouse, Oswald ran from a warehouse to a theatre
Lincoln had two sons, Robert and Edward. Edward died young Robert lived on. Kennedy had two brothers named Robert and Edward. Robert died young and Edward lived on

It seems that these facts are too coincidental¹. Certainly there must be some conspiracy, right?

Well...no. The truth is our minds are just very good at recognizing patterns. If information is missing our minds fill in the missing pieces. If two things are similar we can easily find more similarities. It's an important evolutionary trait. As early hunter/gatherers we needed to understand migration patterns of animals, we needed to recognize which berries made us sick, and we needed to predict the weather. We developed a pattern-seeking mind.

Of course, patterns don't always mean something and our pattern-seeking mind is ultra-sensitive. We see figures in the clouds, we think things like homeopathy are really helping us, and we are really bad at understanding coincidences.

As an example: How many people would you have to put in the same room until it is more than likely that two of them have the same birthday? Your pattern-seeking mind may want to say it would be about 180. If every birthday is equally likely, then birthday will be spread "randomly" throughout the year. It will become more likely than not to share a birthday once more than half of the days are taken. The truth may surprise you - choose 23 people and it is more than likely that 2 of them will share a birthday.

Even more surprising, choose 57 people and there is a 99% chance that 2 of them will share a birthday. Even armed with this knowledge you will still be surprised the next time you meet someone that shares your birthday. For exaple, did you know that in my high school I shared a birthday with 4 of my friends? Also, did you know that Sam, the only other contributor to this blog, has a birthday only one day away from mine?

It is for this reason that antectodal evidence is so dangerous. Our minds are so quick to make associations and doesn't really have a system in place to block false associations. We even make "close enough" associations, as in my birthday example above. If I allow a birthday being only one day off to count as "close enough" then the odds of sharing a birthday increase².

So, no. There is no Lincoln/Kennedy conspiracy, it's not weird that we share a birthday, and evidence is very important.

Notes

[1] Also...some of them are completely made up. However, if you were willing to believe them that just strengthens my argument.

[2] In a group of only 7 people it is more than likely that 2 of them will have a birthday within one week of each other. It is these "close enough" guesses that make psychics lots of money. When a grieving relative is willing to see a false association the odds of appearing psychic increase.

If you have a comment or a question, head over to my